 |
|---|
 |
 |
これは日々の作業を通して学んだことや毎日の生活で気づいたことをを記録しておく備忘録である。
HTML ファイル生成日時: 2026/02/26 20:12:16.296 (台灣標準時)
Scipy の scipy.integrate.solve_ivp を使って Lane-Emden 方程式を数値的 に解いてみたでござる。コードは以下の通りにござる。同じコードを GitHub にも置いておいたでござる。
#!/usr/pkg/bin/python3.9 # # Time-stamp: <2022/05/02 20:15:11 (CST) daisuke> # # importing argparse module import argparse # importing sys module import sys # importing pathlib module import pathlib # importing numpy module import numpy # importing scipy module import scipy.integrate # initialising a parser desc = 'solving Lane-Emden equation numerically' parser = argparse.ArgumentParser (description=desc) # adding arguments parser.add_argument ('-n', '--n', type=float, default=0.0, help='index n of polytrope (default: 0.0)') parser.add_argument ('-s', '--step', type=float, default=0.00001, help='step size of radius (default: 0.00001)') parser.add_argument ('-o', '--output', default='', \ help='output file name') # parsing arguments args = parser.parse_args () # parameters n = args.n step = args.step file_output = args.output # existence check of output file path_output = pathlib.Path (file_output) if (path_output.exists ()): # printing message print ("ERROR: output file '%s' exists, exiting...") # exit sys.exit () # check of polytropic index n if (n > 4.95): # printing message print ("ERROR: choose polytropic index between 0 and 4.95, exiting...") # exit sys.exit () # # Lane-Emden equation # def laneemden (t, y): # making a list with a dimension same as y dy = numpy.zeros_like (y) # Lane-Emden equation dy[0] = y[1] dy[1] = -y[0]**n - 2.0 * y[1] / t # returning values return dy # # event trigger # def cross_zero (t, y): return y[0] cross_zero.terminal = True cross_zero.direction = -1 # initial values y_init = [ 1.0, 0.0 ] # output dimensionless radius values xi_max = 350.0 n_step = int (xi_max / step) t_eval = numpy.linspace (step, xi_max, n_step) # solving equation sol = scipy.integrate.solve_ivp (laneemden, [step, xi_max], y_init, \ t_eval=t_eval, dense_output=True, \ events=cross_zero, \ rtol=10**-12, atol=10**-15) # quick-and-dirty job for finding the surface for i in range ( len (sol.y[0]) ): if (sol.y[0][i] > 0.0): xi_surface = (i+1)*step else: break with open (file_output, 'w') as fh: # writing a header header = "#\n" header += "# xi, theta, r_over_R, rho_over_rho_c, P_over_P_c\n" header += "#\n" header += "# polytropic index n = %f\n" % n header += "# xi_surface = %f\n" % xi_surface header += "#\n" fh.write (header) # printing results for i in range ( len (sol.y[0]) ): # xi xi = (i + 1) * step # theta theta = sol.y[0][i] # stop writing data if theta is negative if (theta < 0.0): break # normalised radius r_over_R = xi / xi_surface # normalised density rho_over_rho_c = theta**n # normalised pressure P_over_P_c = theta**(n+1) # output data data = "%15.13f %15.13f %15.13f %15.13f %15.13f\n" \ % (xi, theta, r_over_R, rho_over_rho_c, P_over_P_c) # writing data to output file fh.write (data)
例えば、 n=3 の場合を計算させるには、以下のようにすればよいでござる。
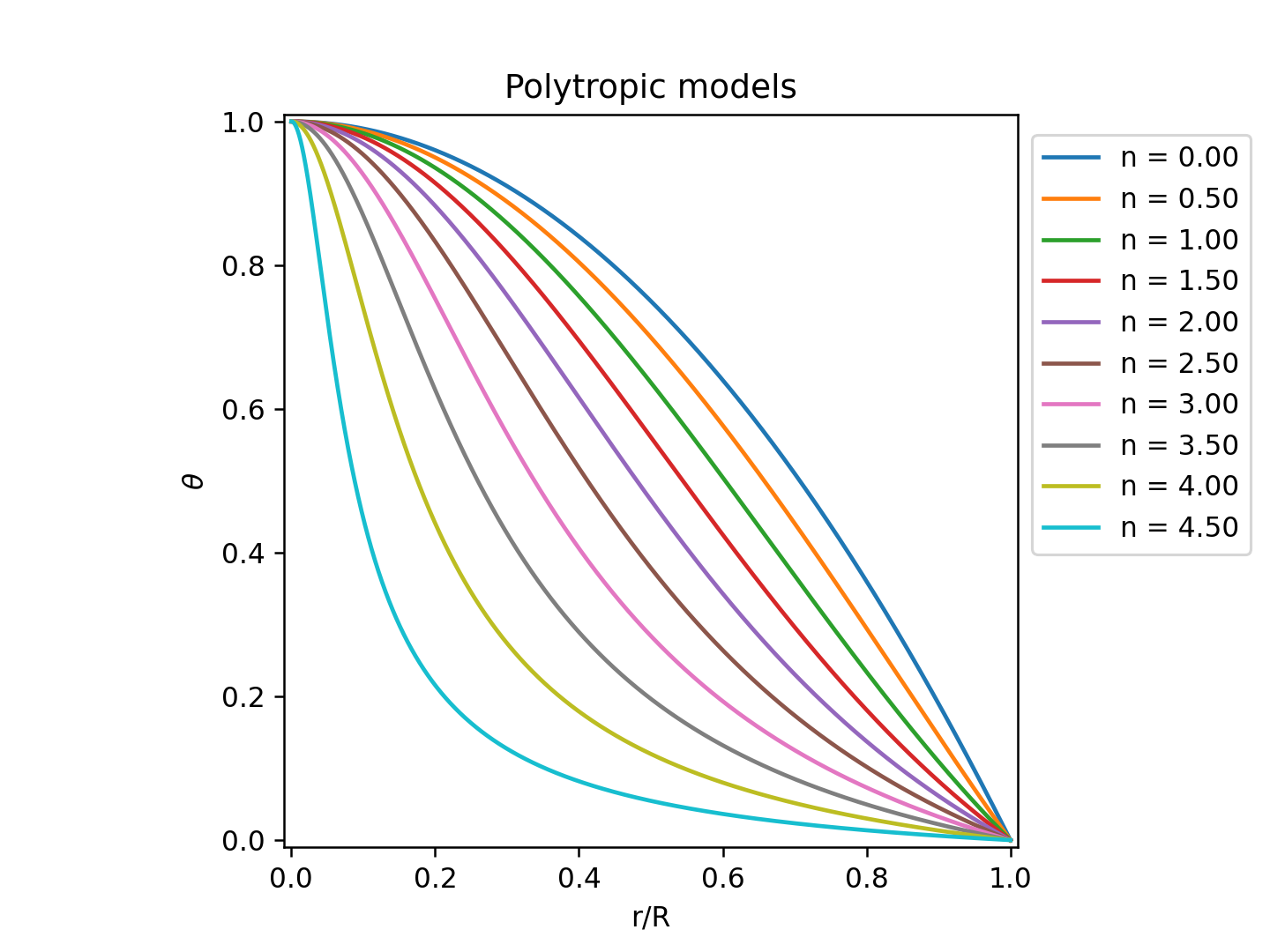
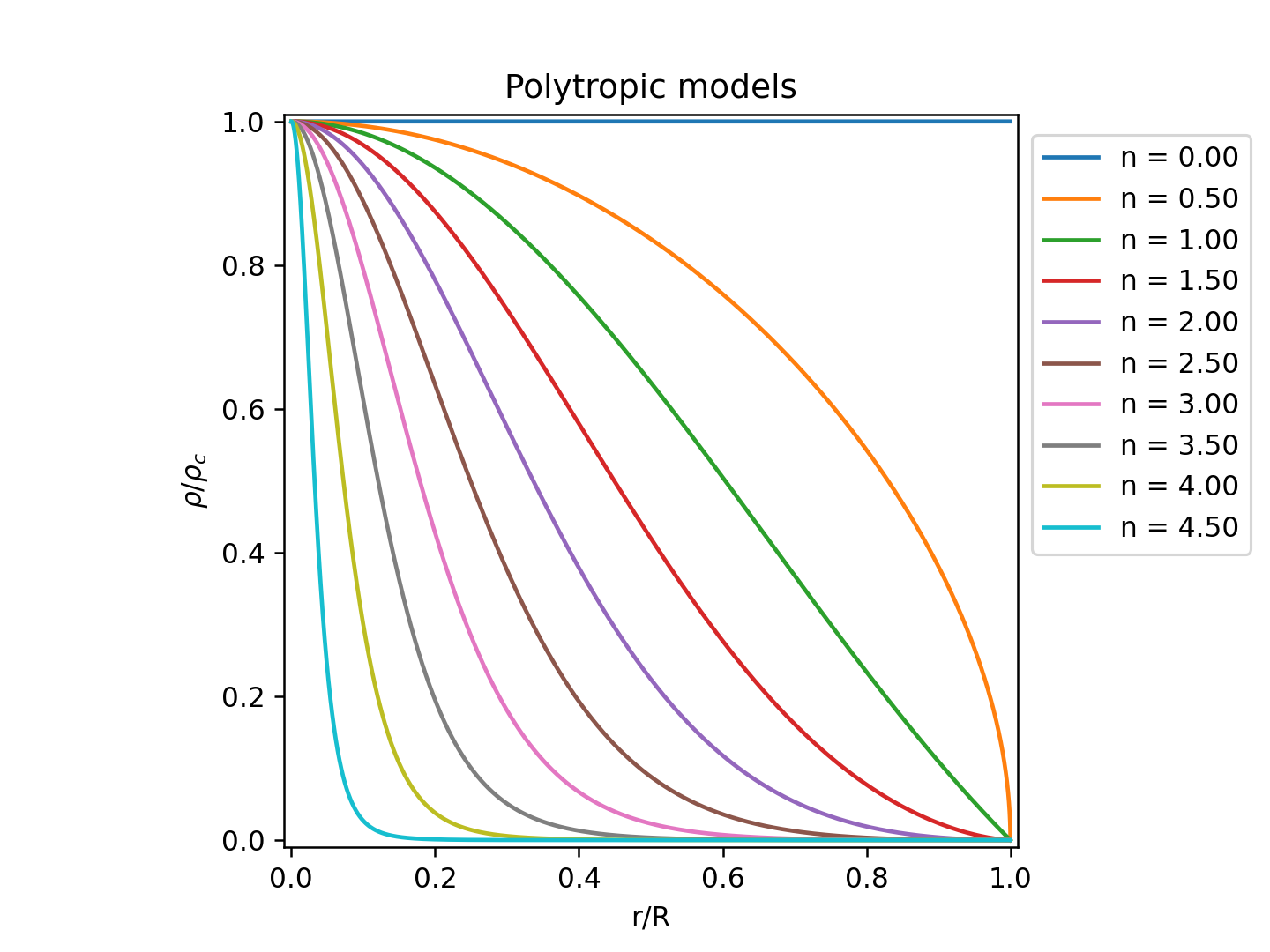
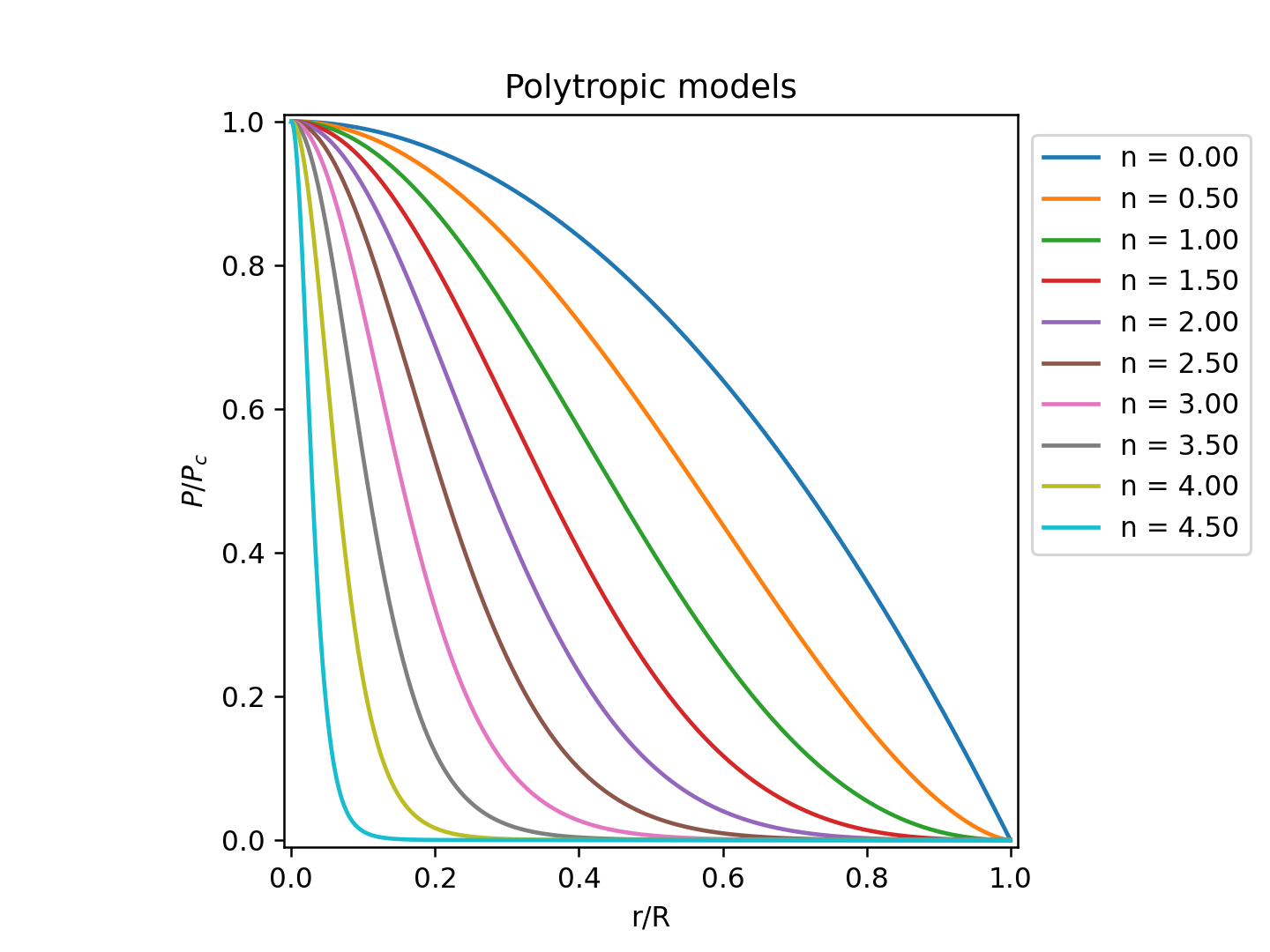
幾つかの polytropic index について計算して、その結果を図にしてみたでご ざる。% ./laneemden.py -n 3.0 -o laneemden_n30.data
 |
|---|
 |
 |