|
|---|
これは日々の作業を通して学んだことや毎日の生活で気づいたことをを記録しておく備忘録である。
HTML ファイル生成日時: 2026/02/26 20:12:16.296 (台灣標準時)
SciPy を使うと、簡便に最小二乗法を利用することができるでござる。まず、 練習用のデータを生成するでござる。以下のようなスクリプトを用意して、実 行してみるでござる。
#!/usr/pkg/bin/python3.9 # # Time-stamp: <2022/07/15 06:42:57 (CST) daisuke> # # importing argparse module import argparse # importing sys module import sys # importing pathlib module import pathlib # importing numpy import numpy # initialising a parser parser = argparse.ArgumentParser (description='plotting data') # adding arguments parser.add_argument ('-a', '--min', type=float, default=0.0, \ help='minimum x value') parser.add_argument ('-b', '--max', type=float, default=100.0, \ help='maximum x value') parser.add_argument ('-s', '--slope', type=float, default=1.0, \ help='gradient of straight line') parser.add_argument ('-i', '--intercept', type=float, default=0.0, \ help='y-intercept of straight line') parser.add_argument ('-e', '--stddev', type=float, default=0.3, \ help='standard deviation of errors') parser.add_argument ('-n', '--ndata', type=int, default=11, \ help='number of data points') # parsing arguments args = parser.parse_args () # input parameters slope = args.slope intercept = args.intercept x_min = args.min x_max = args.max stddev = args.stddev n_data = args.ndata # a function for straight line def func (x, a, b): y = a * x + b return (y) # random number generator rng = numpy.random.default_rng () # generation of synthetic data data_err = rng.normal (0.0, stddev, n_data) data_x = numpy.linspace (x_min, x_max, n_data) data_y = func (data_x, slope, intercept) + data_err # printing generated synthetic data for i in range ( len (data_x) ): print ("%8.4f %8.4f %8.4f" % (data_x[i], data_y[i], stddev) )
以下のように実行してみるでござる。
% ./gen_data.py -s 2 -i 5 -a 0 -b 45 -n 10 -e 0.3 > sample.data % ./gen_data.py -s 2 -i 5 -a 50 -b 70 -n 5 -e 7 >> sample.data % ./gen_data.py -s 2 -i 5 -a 75 -b 100 -n 6 -e 0.3 >> sample.data % cat sample.data 0.0000 5.0030 0.3000 5.0000 14.9402 0.3000 10.0000 25.0036 0.3000 15.0000 35.5060 0.3000 20.0000 44.6728 0.3000 25.0000 55.1272 0.3000 30.0000 65.2244 0.3000 35.0000 74.8133 0.3000 40.0000 84.9241 0.3000 45.0000 94.9772 0.3000 50.0000 108.7896 7.0000 55.0000 121.2910 7.0000 60.0000 116.7390 7.0000 65.0000 137.1529 7.0000 70.0000 139.2072 7.0000 75.0000 154.6195 0.3000 80.0000 164.8580 0.3000 85.0000 175.3297 0.3000 90.0000 185.1314 0.3000 95.0000 194.2291 0.3000 100.0000 205.0442 0.3000
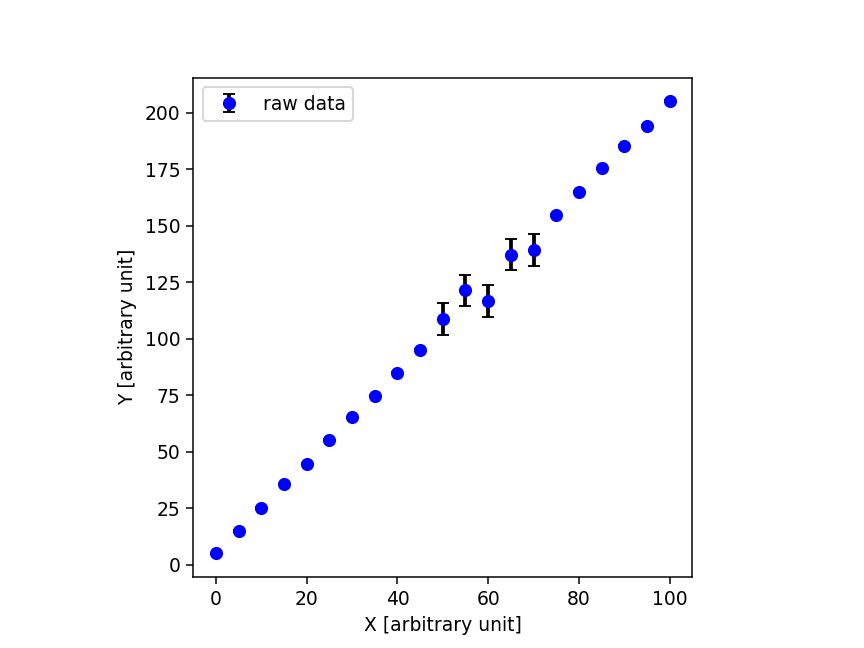
生成したデータを表示してみるでござる。
#!/usr/pkg/bin/python3.9 # # Time-stamp: <2022/07/15 06:43:28 (CST) daisuke> # # importing argparse module import argparse # importing sys module import sys # importing pathlib module import pathlib # importing numpy module import numpy # importing matplotlib module import matplotlib.figure import matplotlib.backends.backend_agg # initialising a parser parser = argparse.ArgumentParser (description='plotting data') # adding arguments parser.add_argument ('-i', '--input', default='sample.data', \ help='input data file name') parser.add_argument ('-o', '--output', default='plot.png', \ help='output image file name') parser.add_argument ('-r', '--resolution', type=float, default=225, \ help='resolution of output image file in DPI') # parsing arguments args = parser.parse_args () # input parameters file_input = args.input file_output = args.output resolution = args.resolution # existence check of files path_input = pathlib.Path (file_input) path_output = pathlib.Path (file_output) if not (path_input.exists ()): print ("ERROR: input file '%s' does not exist." % (file_input) ) sys.exit () if (path_output.exists ()): print ("ERROR: output file '%s' exists." % (file_output) ) sys.exit () if not ( (path_output.suffix == '.eps') \ or (path_output.suffix == '.pdf') \ or (path_output.suffix == '.png') \ or (path_output.suffix == '.ps') ): print ("ERROR: output file must be either EPS, PDF, PNG, or PS file.") sys.exit () # making empty arrays data_x = numpy.array ([]) data_y = numpy.array ([]) data_yerr = numpy.array ([]) # opening input data file with open (file_input, 'r') as fh: # reading file line-by-line for line in fh: # splitting a line (x_str, y_str, yerr_str) = line.split () # converting string into float x = float (x_str) y = float (y_str) yerr = float (yerr_str) # appending data into arrays data_x = numpy.append (data_x, x) data_y = numpy.append (data_y, y) data_yerr = numpy.append (data_yerr, yerr) # making objects "fig" and "ax" fig = matplotlib.figure.Figure () matplotlib.backends.backend_agg.FigureCanvasAgg (fig) ax = fig.add_subplot (111) # axes ax.set_xlabel ("X [arbitrary unit]") ax.set_ylabel ("Y [arbitrary unit]") ax.set_box_aspect (1) # plotting data ax.errorbar (data_x, data_y, yerr=data_yerr, marker='o', color='blue', \ linestyle='None', ecolor='black', elinewidth=2, capsize=3, \ label='raw data') ax.legend () # saving file fig.savefig (file_output, dpi=resolution)
実行してみると、以下のような図ができるでござる。
% ./plot_data.py -i sample.data -o sample.png -r 135 % ls -l sample.* -rw-r--r-- 1 daisuke taiwan 567 Jul 15 06:50 sample.data -rw-r--r-- 1 daisuke taiwan 27890 Jul 15 06:50 sample.png % feh -dF sample.png

|
|---|
scipy.optimize.curve_fit を使って最小二乗法を行ってみるでござる。コー ドは以下の通りにござる。
#!/usr/pkg/bin/python3.9 # # Time-stamp: <2022/07/15 06:53:39 (CST) daisuke> # # importing argparse module import argparse # importing sys module import sys # importing pathlib module import pathlib # importing numpy module import numpy # importing scipy import scipy.optimize # importing matplotlib module import matplotlib.figure import matplotlib.backends.backend_agg # initialising a parser parser = argparse.ArgumentParser (description='fitting data using curve_fit') # adding arguments parser.add_argument ('-i', '--input', default='sample.data', \ help='input file') parser.add_argument ('-o', '--output', default='fitting.png', \ help='output file') parser.add_argument ('-a', '--ainit', type=float, default=1.0, \ help='initial guess of a') parser.add_argument ('-b', '--binit', type=float, default=1.0, \ help='initial guess of b') parser.add_argument ('-r', '--resolution', type=float, default=225, \ help='resolution of output image file in DPI') # parsing arguments args = parser.parse_args () # input parameters file_input = args.input file_output = args.output a_init = args.ainit b_init = args.binit resolution = args.resolution # other parameters n_data = 1000 # existence check of files path_input = pathlib.Path (file_input) path_output = pathlib.Path (file_output) if not (path_input.exists ()): print ("ERROR: input file '%s' does not exist." % (file_input) ) sys.exit () if (path_output.exists ()): print ("ERROR: output file '%s' exists." % (file_output) ) sys.exit () if not ( (path_output.suffix == '.eps') \ or (path_output.suffix == '.pdf') \ or (path_output.suffix == '.png') \ or (path_output.suffix == '.ps') ): print ("ERROR: output file must be either EPS, PDF, PNG, or PS file.") sys.exit () # making empty arrays data_x = numpy.array ([]) data_y = numpy.array ([]) data_yerr = numpy.array ([]) # opening input data file with open (file_input, 'r') as fh: # reading file line-by-line for line in fh: # splitting a line (x_str, y_str, yerr_str) = line.split () # converting string into float x = float (x_str) y = float (y_str) yerr = float (yerr_str) # appending data into arrays data_x = numpy.append (data_x, x) data_y = numpy.append (data_y, y) data_yerr = numpy.append (data_yerr, yerr) # a function for straight line def func (x, a, b): y = a * x + b return (y) # initial guess of coefficients param0 = [a_init, b_init] # weighted least-squares fitting # x: data_x # y: data_y # yerr: data_yerr popt, pcov = scipy.optimize.curve_fit (func, data_x, data_y, p0=param0, \ sigma=data_yerr) # fitted parameters and covariance matrix print ("popt:", popt) print ("pcov:", pcov) # fitted a and b a_fitted, b_fitted = popt # degrees of freedom dof = len (data_x) - len (popt) print ("dof = %d" % (dof) ) # residual and reduced chi-squared residual = ( data_y - func (data_x, a_fitted, b_fitted) ) / data_yerr reduced_chi2 = (residual**2).sum () / dof print ("reduced chi^2 = %f" % (reduced_chi2) ) # errors of a and b a_err, b_err = numpy.sqrt ( numpy.diagonal (pcov) ) print ("a = %f +/- %f (%f %%)" % (a_fitted, a_err, a_err / a_fitted * 100.0) ) print ("b = %f +/- %f (%f %%)" % (b_fitted, b_err, b_err / b_fitted * 100.0) ) # range of data x_min = numpy.amin (data_x) x_max = numpy.amax (data_x) # fitted line fitted_x = numpy.linspace (x_min, x_max, n_data) fitted_y = func (fitted_x, a_fitted, b_fitted) # making objects "fig" and "ax" fig = matplotlib.figure.Figure () matplotlib.backends.backend_agg.FigureCanvasAgg (fig) ax = fig.add_subplot (111) # axes ax.set_title ("least-squares method using curve_fit") ax.set_xlabel ("X [arbitrary unit]") ax.set_ylabel ("Y [arbitrary unit]") ax.set_box_aspect (1) # plotting data ax.errorbar (data_x, data_y, yerr=data_yerr, marker='o', color='blue', \ linestyle='None', ecolor='black', elinewidth=2, capsize=3, \ label='raw data') ax.plot (fitted_x, fitted_y, color='red', \ linestyle='--', linewidth=2, label='fitted function') ax.legend () # saving file fig.savefig (file_output, dpi=resolution)

|
|---|
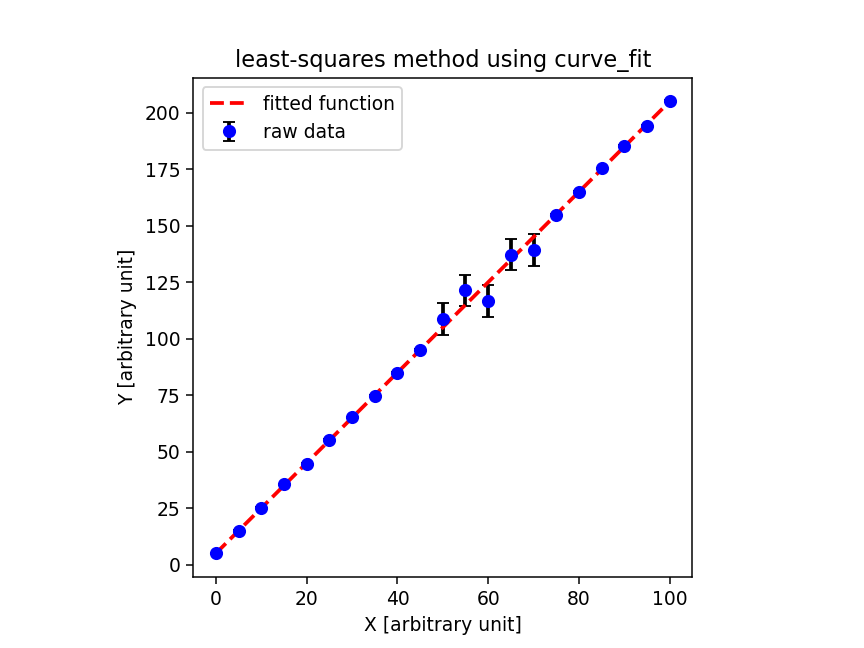
実行結果は以下の通りにござる。 curve_fit を使うと、フィッティングによ り求まった係数の値に加えて、共分散行列も返してくれるので、便利にござる。 共分散行列の対角成分の平方根を取ればフィッティングにより求めた係数の誤 差がわかるでござる。ただ、 degrees of freedom や reduced chi-squared などは自分で計算する必要があるでござる。
% ./fit_curve_fit.py -i sample.data -o curve_fit.png -r 135 popt: [1.99776157 5.06748716] pcov: [[ 4.42292464e-06 -2.07357894e-04] [-2.07357894e-04 1.47899332e-02]] dof = 19 reduced chi^2 = 0.901579 a = 1.997762 +/- 0.002103 (0.105272 %) b = 5.067487 +/- 0.121614 (2.399885 %) % ls -l curve_fit.png -rw-r--r-- 1 daisuke taiwan 41594 Jul 15 06:53 curve_fit.png % feh -dF curve_fit.png
|
|---|
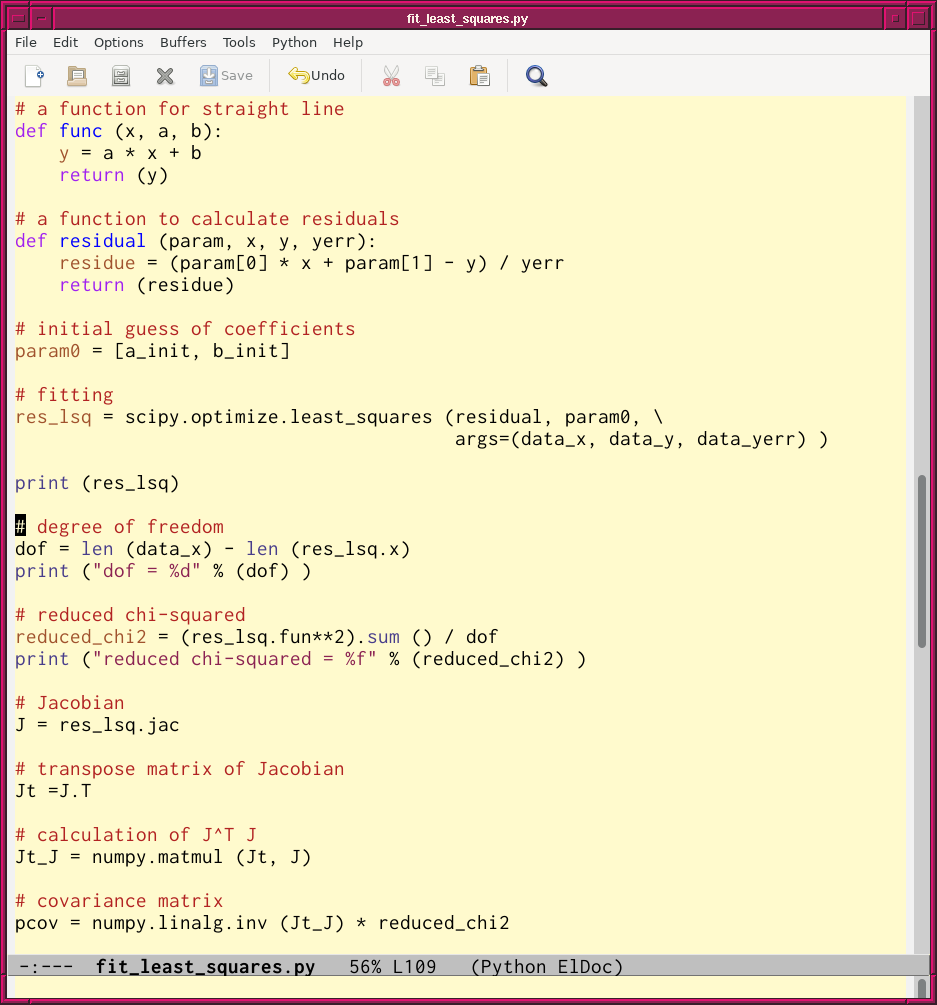
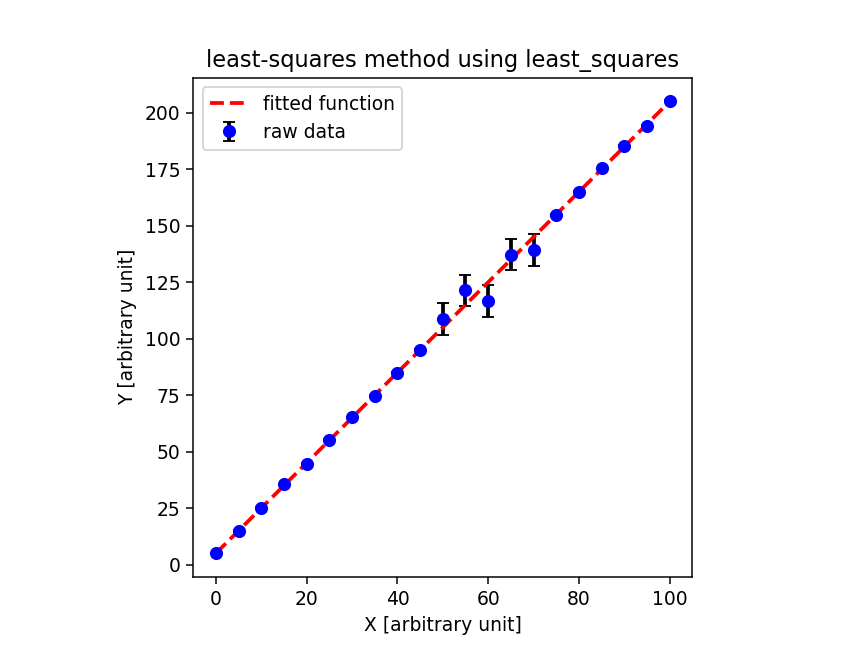
次に、 scipy.optimize.least_squares を使って最小二乗法を行ってみるでご ざる。コードは以下の通りにござる。
#!/usr/pkg/bin/python3.9 # # Time-stamp: <2022/07/15 06:54:29 (CST) daisuke> # # importing argparse module import argparse # importing sys module import sys # importing pathlib module import pathlib # importing numpy module import numpy # importing scipy import scipy.optimize # importing matplotlib module import matplotlib.figure import matplotlib.backends.backend_agg # initialising a parser parser = argparse.ArgumentParser (description='fitting data using least_squares') # adding arguments parser.add_argument ('-i', '--input', default='sample.data', \ help='input file') parser.add_argument ('-o', '--output', default='fitting.png', \ help='output file') parser.add_argument ('-a', '--ainit', type=float, default=1.0, \ help='initial guess of a') parser.add_argument ('-b', '--binit', type=float, default=1.0, \ help='initial guess of b') parser.add_argument ('-r', '--resolution', type=float, default=225, \ help='resolution of output image file in DPI') # parsing arguments args = parser.parse_args () # input parameters file_input = args.input file_output = args.output a_init = args.ainit b_init = args.binit resolution = args.resolution # other parameters n_point = 1000 # existence check of files path_input = pathlib.Path (file_input) path_output = pathlib.Path (file_output) if not (path_input.exists ()): print ("ERROR: input file '%s' does not exist." % (file_input) ) sys.exit () if (path_output.exists ()): print ("ERROR: output file '%s' exists." % (file_output) ) sys.exit () if not ( (path_output.suffix == '.eps') \ or (path_output.suffix == '.pdf') \ or (path_output.suffix == '.png') \ or (path_output.suffix == '.ps') ): print ("ERROR: output file must be either EPS, PDF, PNG, or PS file.") sys.exit () # making empty arrays data_x = numpy.array ([]) data_y = numpy.array ([]) data_yerr = numpy.array ([]) # opening input data file with open (file_input, 'r') as fh: # reading file line-by-line for line in fh: # splitting a line (x_str, y_str, yerr_str) = line.split () # converting string into float x = float (x_str) y = float (y_str) yerr = float (yerr_str) # appending data into arrays data_x = numpy.append (data_x, x) data_y = numpy.append (data_y, y) data_yerr = numpy.append (data_yerr, yerr) # a function for straight line def func (x, a, b): y = a * x + b return (y) # a function to calculate residuals def residual (param, x, y, yerr): residue = (param[0] * x + param[1] - y) / yerr return (residue) # initial guess of coefficients param0 = [a_init, b_init] # fitting res_lsq = scipy.optimize.least_squares (residual, param0, \ args=(data_x, data_y, data_yerr) ) print (res_lsq) # degree of freedom dof = len (data_x) - len (res_lsq.x) print ("dof = %d" % (dof) ) # reduced chi-squared reduced_chi2 = (res_lsq.fun**2).sum () / dof print ("reduced chi-squared = %f" % (reduced_chi2) ) # Jacobian J = res_lsq.jac # transpose matrix of Jacobian Jt =J.T # calculation of J^T J Jt_J = numpy.matmul (Jt, J) # covariance matrix pcov = numpy.linalg.inv (Jt_J) * reduced_chi2 # printing covariance matrix print ("pcov =", pcov) # fitted a and b a_fitted, b_fitted = res_lsq.x a_err, b_err = numpy.sqrt ( numpy.diagonal (pcov) ) print ("a = %f +/- %f (%f %%)" % (a_fitted, a_err, a_err / a_fitted * 100.0) ) print ("b = %f +/- %f (%f %%)" % (b_fitted, b_err, b_err / b_fitted * 100.0) ) # range of data x_min = numpy.amin (data_x) x_max = numpy.amax (data_x) # fitted line fitted_x = numpy.linspace (x_min, x_max, n_point) fitted_y = func (fitted_x, a_fitted, b_fitted) # making objects "fig" and "ax" fig = matplotlib.figure.Figure () matplotlib.backends.backend_agg.FigureCanvasAgg (fig) ax = fig.add_subplot (111) # axes ax.set_title ("least-squares method using least_squares") ax.set_xlabel ("X [arbitrary unit]") ax.set_ylabel ("Y [arbitrary unit]") ax.set_box_aspect (1) # plotting data ax.errorbar (data_x, data_y, yerr=data_yerr, marker='o', color='blue', \ linestyle='None', ecolor='black', elinewidth=2, capsize=3, \ label='raw data') ax.plot (fitted_x, fitted_y, color='red', \ linestyle='--', linewidth=2, label='fitted function') ax.legend () # saving file fig.savefig (file_output, dpi=resolution)
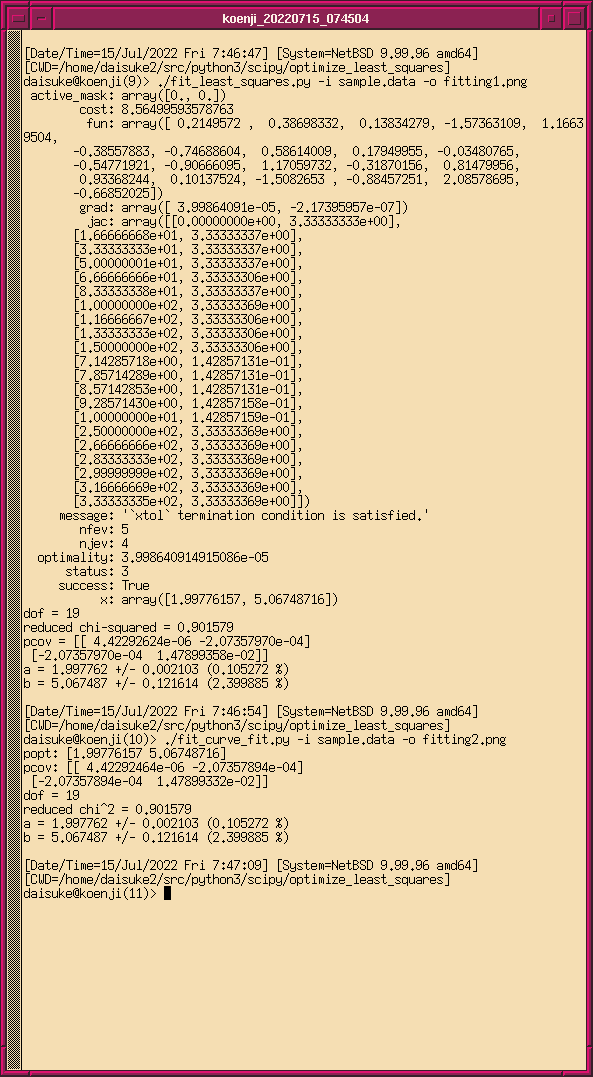
実行結果は以下の通りにござる。 least_squares を使うと、フィッティング により求めた係数の値とヤコビアンが得られるでござる。ヤコビアンから共分 散行列を求めるところは自分で行う必要があるでござる。ヤコビアン J の転 置行列を作り、ヤコビアンの転置行列とヤコビアンの掛け算をし、その逆行列 を作り、 reduced chi-squared を掛ければ、共分散行列が得られるでござる。
% ./fit_least_squares.py -i sample.data -o least_squares.png -r 135 active_mask: array([0., 0.]) cost: 8.56499593578763 fun: array([ 0.2149572 , 0.38698332, 0.13834279, -1.57363109, 1.16639504, -0.38557883, -0.74688604, 0.58614009, 0.17949955, -0.03480765, -0.54771921, -0.90666095, 1.17059732, -0.31870156, 0.81479956, 0.93368244, 0.10137524, -1.5082653 , -0.88457251, 2.08578695, -0.66852025]) grad: array([ 3.99864091e-05, -2.17395957e-07]) jac: array([[0.00000000e+00, 3.33333333e+00], [1.66666668e+01, 3.33333337e+00], [3.33333333e+01, 3.33333337e+00], [5.00000001e+01, 3.33333337e+00], [6.66666666e+01, 3.33333306e+00], [8.33333338e+01, 3.33333337e+00], [1.00000000e+02, 3.33333369e+00], [1.16666667e+02, 3.33333306e+00], [1.33333333e+02, 3.33333306e+00], [1.50000000e+02, 3.33333306e+00], [7.14285718e+00, 1.42857131e-01], [7.85714289e+00, 1.42857131e-01], [8.57142853e+00, 1.42857131e-01], [9.28571430e+00, 1.42857158e-01], [1.00000000e+01, 1.42857159e-01], [2.50000000e+02, 3.33333369e+00], [2.66666666e+02, 3.33333369e+00], [2.83333333e+02, 3.33333369e+00], [2.99999999e+02, 3.33333369e+00], [3.16666669e+02, 3.33333369e+00], [3.33333335e+02, 3.33333369e+00]]) message: '`xtol` termination condition is satisfied.' nfev: 5 njev: 4 optimality: 3.998640914915086e-05 status: 3 success: True x: array([1.99776157, 5.06748716]) dof = 19 reduced chi-squared = 0.901579 pcov = [[ 4.42292624e-06 -2.07357970e-04] [-2.07357970e-04 1.47899358e-02]] a = 1.997762 +/- 0.002103 (0.105272 %) b = 5.067487 +/- 0.121614 (2.399885 %)
|
|---|
|
|---|
|
|---|
そうなってもらわねば困るのでござるが、 curve_fit と least_squares とで 同じ結果が得られたでござる。
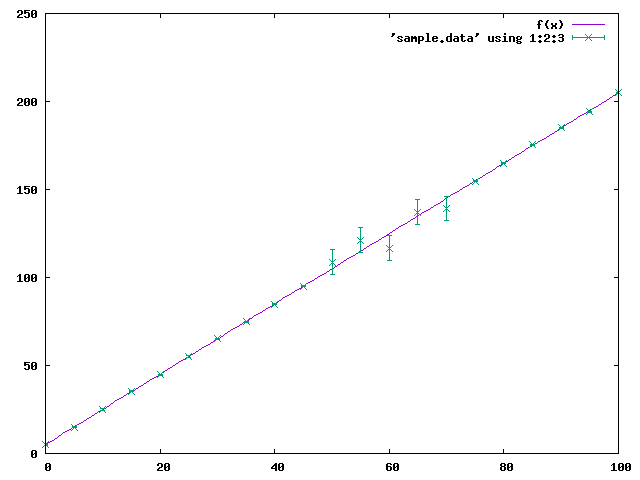
最後に、確認のため、 gnuplot の fit を使って最小二乗法を行ってみるでご ざる。
% gnuplot G N U P L O T Version 5.4 patchlevel 2 last modified 2021-06-01 Copyright (C) 1986-1993, 1998, 2004, 2007-2021 Thomas Williams, Colin Kelley and many others gnuplot home: http://www.gnuplot.info faq, bugs, etc: type "help FAQ" immediate help: type "help" (plot window: hit 'h') Terminal type is now 'x11' gnuplot> f(x) = a*x+b gnuplot> fit f(x) 'sample.data' using 1:2:3 yerror via a,b iter chisq delta/lim lambda a b 0 6.6280641360e+05 0.00e+00 1.19e+02 1.000000e+00 1.000000e+00 1 1.3677713248e+03 -4.84e+07 1.19e+01 2.029816e+00 1.031804e+00 2 5.0241098542e+02 -1.72e+05 1.19e+00 2.037318e+00 2.246001e+00 3 1.7380405903e+01 -2.79e+06 1.19e-01 1.998660e+00 5.003394e+00 4 1.7129991885e+01 -1.46e+03 1.19e-02 1.997762e+00 5.067472e+00 5 1.7129991872e+01 -7.89e-05 1.19e-03 1.997762e+00 5.067487e+00 iter chisq delta/lim lambda a b After 5 iterations the fit converged. final sum of squares of residuals : 17.13 rel. change during last iteration : -7.8942e-10 degrees of freedom (FIT_NDF) : 19 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.949515 variance of residuals (reduced chisquare) = WSSR/ndf : 0.901579 p-value of the Chisq distribution (FIT_P) : 0.581061 Final set of parameters Asymptotic Standard Error ======================= ========================== a = 1.99776 +/- 0.002103 (0.1053%) b = 5.06749 +/- 0.1216 (2.4%) correlation matrix of the fit parameters: a b a 1.000 b -0.811 1.000 gnuplot> plot f(x), 'sample.data' using 1:2:3 with yerrorbar gnuplot> set term png medium Terminal type is now 'png' Options are 'nocrop enhanced size 640,480 medium ' gnuplot> set output 'fit_gnuplot.png' gnuplot> replot gnuplot> quit

|
|---|
|
|---|
gnuplot による結果も curve_fit 及び least_squares と同じになったでござ る。